[Discrete Mathematics] Basic Structures : Sets, Functions, Sequences, Sums, and Matrices
1. Sets
2. Set Operations
2.1 Introduction
Two, or more, sets can be combined in many differenct ways.
[Definition 1]
Let $A$ and $B$ be sets. The union of the sets $A$ and $B$, denoted by $A \cup B$, is the set that contains those elements that are either in $A$ or in $B$, or in both.
[Definition 2]
Let $A$ and $B$ be sets. The intersection of the sets $A$ and $B$, denoted by $A \cap B$, is the set that contains those elements that are in both $A$ and in $B$.
[Definition 3]
Two sets are called disjoint if their intersection is the empty set.
[Definition 4]
[Definition 5]
2.2 Set Identities
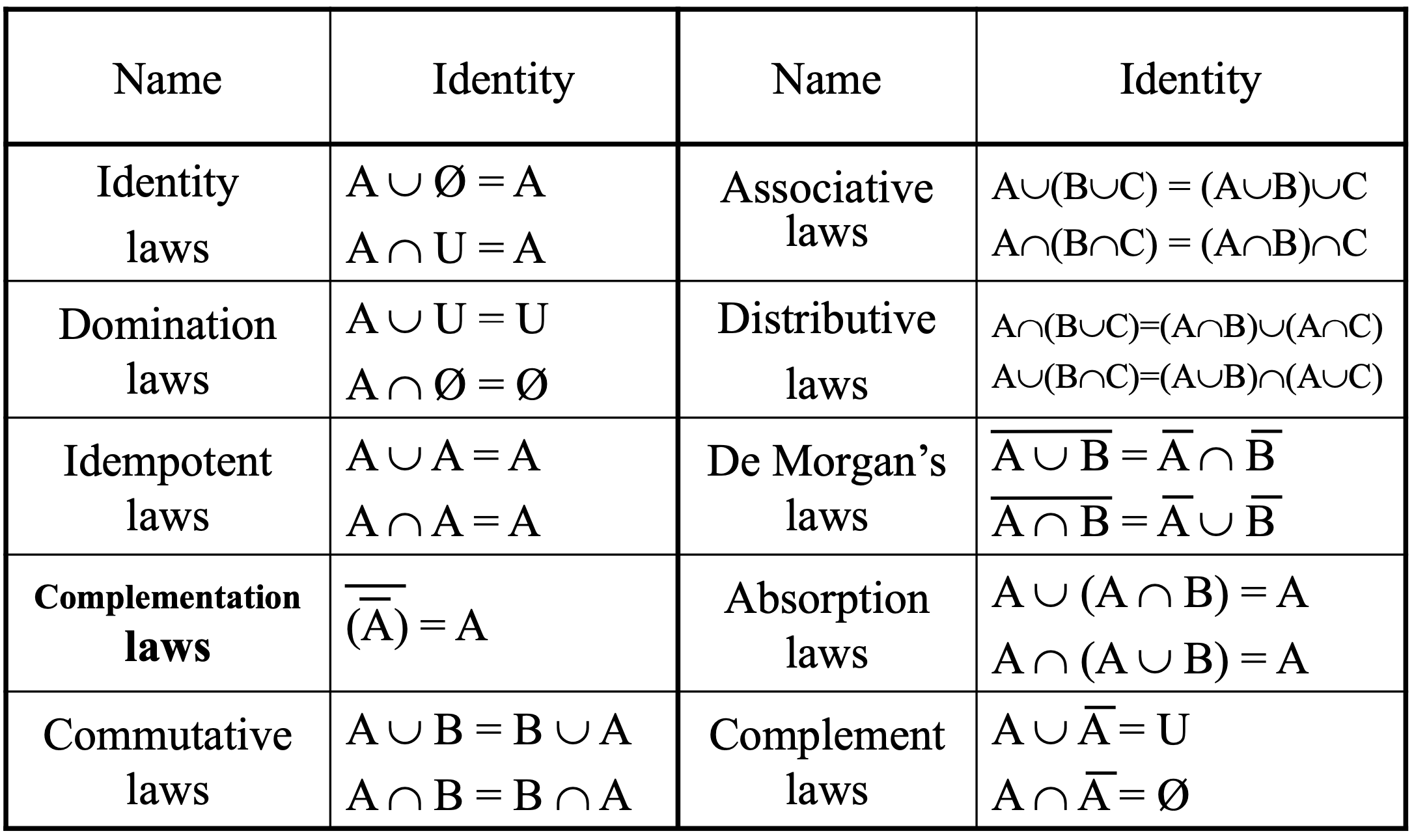
2.3 Generalized Unions and Intersections
2.4 Computer Represetation of Sets
A method for storing elements using an arbitrary ordering of the elements of the universal set.
- Assume that the universal set $U$ is finite.
- Specify an arbitrary ordering of the elements of $U$, for instance $a_1, a_2, …, a_n$.
- Represent a subset $A$ of $U$ with the bit string of length $n$, where the $i$th bit in this string is 1 if $a_i$ belongs to $A$ and is 0 if $a_i$ does not belong to $A$.
let bit strings of $U$ is 1111 1111 1111 1111 1111 1111 11, bit strings of {a, b, c, d, e} is 1111 1000 0000 0000 0000 0000 00
2.5 Multisets
3. Functions
3.1 Introduction
[Definition 1] Let $A$ and $B$ be sets. A function f from $A$ to $B$ is an assignment of exactly on element of $B$ to each element of $A$. We write $f(a) = b$ if $b$ is the unique element of $B$ assigend by the function $f$ to the element $a$ of $A$. If $f$ is a function from $A$ to $B$, we write $f : A \rightarrow B$.
3.2 One-to-One and Onto Functions
[Definition 5] A function $f$ is said to be one-to-one, or an injection, if and only if $f(a) = f(b)$ implies that $a = b$ for all $a$ and $b$ in the domain of $f$. A function is said to be injective if it is one-to-one.
[Definition 7] A function $f$ from $A$ to $B$ is called onto, or a surjection, if and only if for every element $b \in B$ there is an element $a \in A$ with $f(a) = b$. A function $f$ is called surjective if it is onto.
3.3 Inverse Functions and Compositions of Functions
[Definition 9] Let $f$ be a one-to-one correspondence from the set $A$ to the set $B$. The inverse function of $f$ is the function that assigns to an element $b$ belonging to $B$ the unique element $a$ in $A$ such that $f(a) = b$. The inverse function of $f$ is denoted by $f^{-1}$. Hence, $f^{-1}(b) = a$ when $f(a) = b$.
[Definition 10] Let $g$ be a function from the set $A$ to the set $B$ and let $f$ be a function from the set $B$ to the set $C$. The composition of the functions $f$ and $g$, denoted for all $a \in A$ by $f \cdot g$, is the function from $A$ to $C$ defined by $(f \cdot g)(a) = f(g(a))$.
3.4 The Graphs of Functions
3.5 Some Important Functions
[Definition 12] The floor function assigns to the real number $x$ the largest integer that is less than or equal to $x$. The value of the floor function at $x$ is denoted by $\lfloor x \rfloor$.
The ceiling function assigns to the real number $x$ the smallest integer that is greater than or equal to $x$. The value of the ceiling function at $x$ is denoted by $\lceil x \rceil$
| Useful Properties of Floor and Ceiling functions. ($n$ is an integer, $x$ is a real number.) |
|---|
| $\lfloor x \rfloor = n$ if and only if $n \leq x < n + 1$ |
| $\lceil n \rceil = n$ if and only if $n-1 < x \leq n$ |
| $\lfloor x \rfloor = n$ if and only if $x-1 < n \leq x$ |
| $\lceil n \rceil = n$ if and only if $x \leq n < n-1$ |
| $x-1 < \lfloor x \rfloor \leq x \leq \lceil x \rceil < x + 1$ |
| $\lfloor -x \rfloor = - \lceil x \rceil$ |
| $\lceil -x \rceil = - \lfloor x \rfloor$ |
| $\lfloor x + n \rfloor = \lfloor x \rfloor + n$ |
| $\lceil x + n \rceil = \lceil x \rceil + n$ |
3.6 Partial Functions
4. Sequences and Summations
5. Cardinality of Sets
5.1 Introduction
[Definition 1] The sets $A$ and $B$ have the same cardinarity if and only if there is a one-to-one corresponence from $A$ to $B$. When $A$ and $B$ have the same cardinarity, we write $|A| = |B|$.
5.2 Countable Sets
[Definition 2] If there is a one-to-one function from $A$ to $B$, the cardinality of $A$ is less that or the same as the cardinality of $B$ and we write $|A| \leq |B|$. Moreover, when $|A| \leq |B|$ and A and B have differenct cardinality, we say that the cardinality of $A$ less than the cardinality of $B$ and we write $|A| < |B|$
[Definition 3] A set that is either finite or has the same cardinality as the set of positive integers is called countable. A set that is not countable is called uncountable.
5.3 An Uncountable Set
6. Matrices
6.4 Zero-One Matrices
Zero-one matrix is a matrix all of whose entries are either 0 or 1.
[Definition 8] Let $A = [a_{ij}]$ and $B = [b_{ij}]$ be $m \times n$ zero-one matrices. Then the join of $A$ and $B$ is denoted by $A \vee B$.
The meet of $A$ and $B$ is the zero matriz with $(i, j)$th entry $a_{ij} \wedge b_{ij}$. The meet of $A$ and $B$ is denoted by $A \wedge B$.
[Definition 9] Let $A = [a_{ij}]$ be an $m \times k$ zero-one matrix and $B = [b_{ij}]$ be a $k \times n$ zero-one matrix. Then the Boolean project of $A$ and $B$, denoted by $A \odot B$, is the $m \times n$ matrix with $(i, j)$th entry $c_{ij}$ where $c_{ij} = (a_{i1} \wedge b_{1j}) \vee (a_{i2} \wedge b_{2j}) \vee … \vee (a_{i3} \wedge b_{3j})$.
[Definition 10] Lat $A$ be a square zero-one matrix and let $r$ be a positive integer. The $r$th Boolean power of $A$ is the Boolean product of $r$ factors of $A$.