[F1tenth] Kinematics and Dynamics of Vehicle
1. Kinematic Bycycle Model (Single Track Model)
Notation
- $x$: absolute position x (m)
- $y$: absolute position y (m)
- $\psi$: yaw (deg)
- $v$: velocity (m/s)
- $\delta$: steering angle (deg)
- $\beta:$ side slip angle
State and action
\[\mathbf{x} = \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5 \\ \end{bmatrix} = \begin{bmatrix} x \\ y \\ \psi \\ v \\ \delta \\ \end{bmatrix}, \;\;\; u = \delta\]Kinematic Bicycle Model
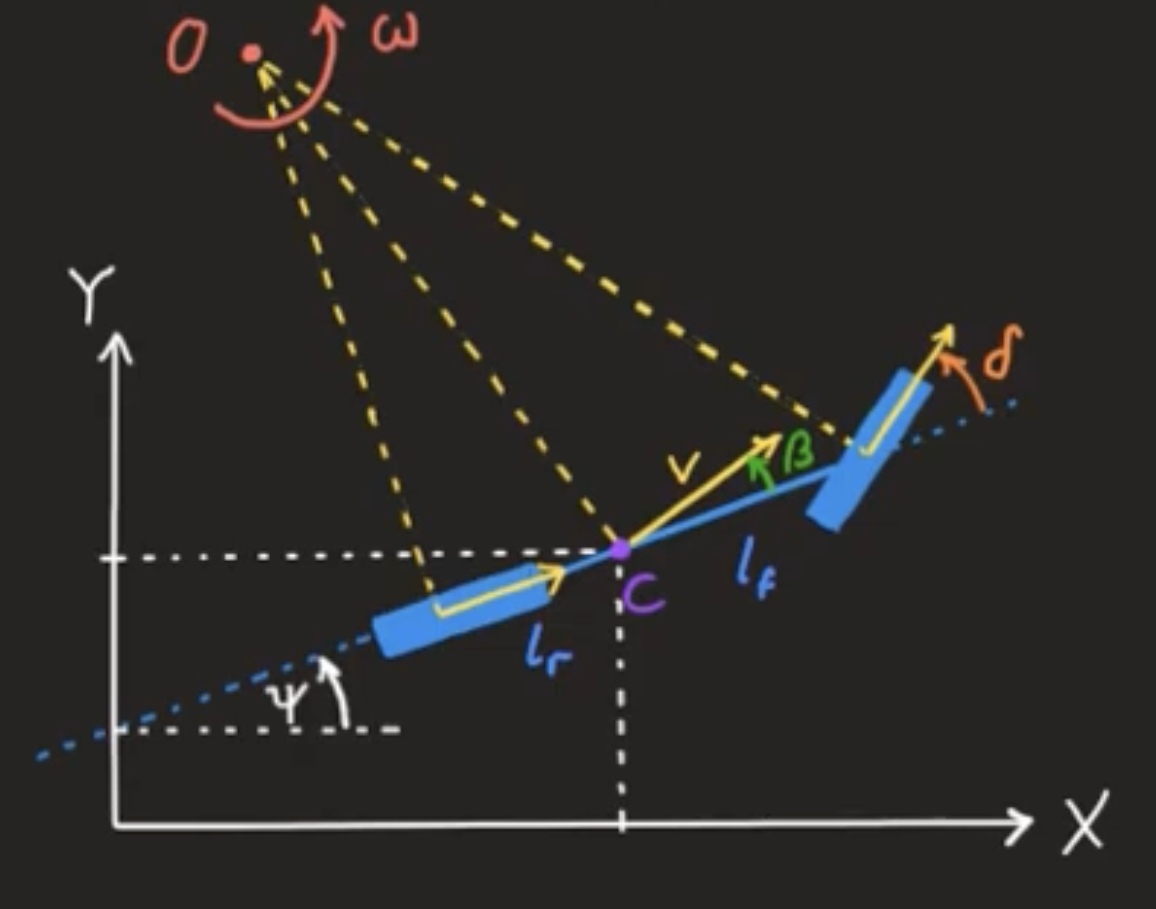
where
\[\beta = \arctan{\left(\dfrac{l_r}{l_r +l_f} \tan\delta\right)}\]Therefore
\[\begin{bmatrix} \dot{x}_1 \\ \dot{x}_2 \\ \dot{x}_3 \\ \dot{x}_4 \\ \dot{x}_5 \\ \end{bmatrix} = \begin{bmatrix} x_4 \cos{\left(x_3 + \arctan{\left(\dfrac{l_r}{l_r +l_f} \tan\delta\right)} \right)} \\ x_4 \sin{\left(x_3 + \arctan{\left(\dfrac{l_r}{l_r +l_f} \tan\delta\right)} \right)} \\ \dfrac{x_4}{l_r + l_f} \cos\left( \arctan{\left(\dfrac{l_r}{l_r +l_f} \tan\delta\right)} \right) \tan\delta \\ \dot{x}_4 \\ \dot{x}_5 \\ \end{bmatrix}\]Implementation
\[\beta = \arctan{\left(\dfrac{l_r}{l_r +l_f} \tan\delta\right)} \\\] \[\begin{bmatrix} \Delta{x_1} \\ \Delta{x_2} \\ \Delta{\psi} \\ \Delta \delta \\ \end{bmatrix} = \begin{bmatrix} v \cos(\psi + \beta) \Delta t\\ v \sin(\psi + \beta) \Delta t \\ \dfrac{v}{l_r + l_f} \cos\beta \tan\delta \Delta t \\ \dfrac{\delta - \delta}{\tau}\Delta t \\ \end{bmatrix}\] \[\begin{bmatrix} x_1(k+1) \\ x_2(k+1) \\ x_3(k+1) \\ x_4(k+1) \\ x_5(k+1) \\ \end{bmatrix} = \begin{bmatrix} x_1(k) + \Delta x_1(k) \\ x_2(k) + \Delta x_2(k) \\ \arctan \left( \dfrac{\sin{(x_3(k) + \Delta x_3(k))}}{\cos{(x_3(k) + \Delta x_3(k))}} \right) \\ x_4(k+1) \\ x_5(k) + \Delta x_5(k) \\ \end{bmatrix}\]- $x_4(k+1) = v(k+1)$ 는 global planner로부터 받은 reference speed를 이용한다. (look-up table)
- $\Delta \delta$ 는 1차 지연을 이용한다.
2. Dynamic Bicycle Model
Notation for state and action
\[\mathbf{x} = \begin{bmatrix} x \\ y \\ v_x \\ v_y \\ \psi \\ \dot{\psi} \\ \end{bmatrix}, \;\;\; u = \delta\]based on the 3 Degrees of Freedom dynamics bicycle model of the vechicle combined with a linear tire model
\[\begin{align*} m(\dot{v}_x - \dot{\psi}v_y) &= F_{xf} + F_{xr} \\ m(\dot{v}_y + \dot{\psi}v_x) &= F_{yf} + F_{yr} \\ I_z \ddot{\psi} &= I_f F_{yf} - I_r F_{yr} \end{align*}\]$C_{\tau}, C_{\alpha}$ corresponds to the longitudinal (lateral) tire stiffness coefficient
\[\begin{align*} F_{xp_f} &= C_{\tau_f}\tau_{x_f} \\ F_{yp_f} &= C_{\alpha_f} \left(\delta_f - \dfrac{v_y + I_f \psi}{v_x} \right) \\ F_{xp_r} &= C_{\tau_r} \tau_{x_r} \\ F_{yp_r} &= - C_{\alpha_r}\left( \dfrac{v_y - I_r \psi}{v_x} \right) \end{align*}\]…
\[\begin{bmatrix} \dot{x} \\ \dot{y} \\ \dot{v_x} \\ \dot{v_y} \\ \dot{\psi} \\ \ddot{\psi} \\ \end{bmatrix} = \begin{bmatrix} v_x \cos{\psi} - v_y \sin{\psi} \\ v_x \sin{\psi} + v_y \cos{\psi} \\ \dfrac{F_{xf} + F_{xr}}{m} + \dot{\psi}v_y \\ \dfrac{F_{yf} + F_{yr}}{m} - \dot{\psi}v_x \\ \dot{\psi} \\ \dfrac{I_f F_{yf} - I_r F_{yr}}{I_z} \\ \end{bmatrix}\]3. Pacejka Magic Tire Formula
- Lookahead point와 현재 위치의 벡터 계산
- 차량의 좌측 방향 벡터
차량의 전방 방향 벡터는 다음과 같다.
\[\vec{d} = \begin{bmatrix} \cos{\psi} \\ \sin{\psi} \\ \end{bmatrix}\]차량의 좌측 방향은 방향 벡터를 90 degree 회전시켜야 한다. 90 degree에 해당하는 회전 행렬을 곱한다.
perpendicular vector는 다음과 같다.
\[\vec{d}_{\bot} = \begin{bmatrix} 0 & -1 \\ 1 & 0 \\ \end{bmatrix} \begin{bmatrix} \cos{\psi} \\ \sin{\psi} \\ \end{bmatrix} = \begin{bmatrix} -\sin{\psi} \\ \cos{\psi} \\ \end{bmatrix}\]- 차량의 측면 각도
lookahead vector를 기준으로 얼마나 벗어났는지를 나타내는 측면 각도를 $\eta$라고 하자.
\[\sin{\eta} = \dfrac{\vec{p} \cdot \vec{d}_{\bot}}{\vert\vert \vec{p} \vert\vert \cdot \vert\vert \vec{d}_{\bot} \vert\vert}\]- 차량의 횡가속도
lateral acceleration
\[a_{\text{lateral}} = 2 \dfrac{v_{\text{target}}^2}{L_1} \sin{\eta}\]- steering angle
where $f$ is a look-up table function. Look-up table function $f$는 pacejka의 magic tire model에서 횡가속도와 조향각 간의 관계를 반영하여 생성되었다.
- command
Implementation
Kinematic Bicycle Model
하나의 state sequence를 예측하는 것이 목적이다.
// Predict both local and global state sequence from control sequence
void MPCBase::predict_state_seq(const ControlSeq& control_seq,
const State& global_init_state,
const grid_map::GridMap& reference_map,
StateSeq* global_state_seq,
StateSeq* local_state_seq) const {
// observed state
global_state_seq->row(0) = global_init_state;
// // observed state
local_state_seq->row(0) = State::Zero(STATE_SPACE::dim);
local_state_seq->row(0)(STATE_SPACE::vel) = global_init_state(STATE_SPACE::vel);
// This is for linear prediction mode of speed
const double init_x = global_init_state(STATE_SPACE::x);
const double init_y = global_init_state(STATE_SPACE::y);
double current_reference_speed = 0;
if (reference_map.isInside(grid_map::Position(init_x, init_y))) {
current_reference_speed = reference_map.atPosition(speed_field_layer_name_, grid_map::Position(init_x, init_y));
}
// double prev_steer_angle = control_seq(0, CONTROL_SPACE::steer);
for (size_t i = 0; i < prediction_step_size_ - 1; i++) {
double steer_angle = 0.0;
if (i <= steer_delay_steps_) {
// To consider input delay
steer_angle = control_seq(0, CONTROL_SPACE::steer);
} else {
steer_angle = control_seq(i, CONTROL_SPACE::steer);
}
// const double steer_angle = control_seq(i, CONTROL_SPACE::steer);
// const double accel = control_seq(i, CONTROL_SPACE::accel);
// Update global state
const double global_x = global_state_seq->row(i)(STATE_SPACE::x);
const double global_y = global_state_seq->row(i)(STATE_SPACE::y);
const double global_yaw = global_state_seq->row(i)(STATE_SPACE::yaw);
const double global_vel = global_state_seq->row(i)(STATE_SPACE::vel);
const double global_steer = global_state_seq->row(i)(STATE_SPACE::steer);
const double beta_global = atan(lf_ / (lf_ + lr_) * tan(global_steer));
// Kinematic Bicycle Model with steer 1st order delay
const double delta_global_x = global_vel * cos(global_yaw + beta_global) * prediction_interval_;
const double delta_global_y = global_vel * sin(global_yaw + beta_global) * prediction_interval_;
const double delta_global_yaw = global_vel * sin(beta_global) / lr_ * prediction_interval_;
const double delta_global_steer = ((steer_angle - global_steer) / steer_delay_tau_) * prediction_interval_;
double next_vel = 0.0;
if (speed_prediction_mode_ == SpeedPredictionMode::CONSTANT) {
next_vel = constant_speed_prediction(global_vel);
} else if (speed_prediction_mode_ == SpeedPredictionMode::LINEAR) {
next_vel = linear_speed_prediction(global_vel, current_reference_speed, prediction_interval_, min_accel_, max_accel_);
} else if (speed_prediction_mode_ == SpeedPredictionMode::REFERENCE) {
next_vel = reference_speed_prediction(global_x, global_y, reference_map);
}
global_state_seq->row(i + 1)(STATE_SPACE::x) = global_x + delta_global_x;
global_state_seq->row(i + 1)(STATE_SPACE::y) = global_y + delta_global_y;
global_state_seq->row(i + 1)(STATE_SPACE::yaw) = std::atan2(sin(global_yaw + delta_global_yaw), cos(global_yaw + delta_global_yaw));
global_state_seq->row(i + 1)(STATE_SPACE::vel) = next_vel;
global_state_seq->row(i + 1)(STATE_SPACE::steer) = global_steer + delta_global_steer;
// Update local state
const double local_x = local_state_seq->row(i)(STATE_SPACE::x);
const double local_y = local_state_seq->row(i)(STATE_SPACE::y);
const double local_yaw = local_state_seq->row(i)(STATE_SPACE::yaw);
const double local_vel = local_state_seq->row(i)(STATE_SPACE::vel);
const double local_steer = local_state_seq->row(i)(STATE_SPACE::steer);
const double beta_local = atan(lf_ / (lf_ + lr_) * tan(local_steer));
// Kinematic Bicycle Model with steer 1st order delay
const double delta_local_x = local_vel * cos(local_yaw + beta_local) * prediction_interval_;
const double delta_local_y = local_vel * sin(local_yaw + beta_local) * prediction_interval_;
const double delta_local_yaw = local_vel * sin(beta_local) / lr_ * prediction_interval_;
const double delta_local_steer = ((steer_angle - local_steer) / steer_delay_tau_) * prediction_interval_;
local_state_seq->row(i + 1)(STATE_SPACE::x) = local_x + delta_local_x;
local_state_seq->row(i + 1)(STATE_SPACE::y) = local_y + delta_local_y;
local_state_seq->row(i + 1)(STATE_SPACE::yaw) = std::atan2(sin(local_yaw + delta_local_yaw), cos(local_yaw + delta_local_yaw));
local_state_seq->row(i + 1)(STATE_SPACE::vel) = next_vel;
local_state_seq->row(i + 1)(STATE_SPACE::steer) = local_steer + delta_local_steer;
}
}
Pacejka Magic Tire Formula
# Vector from the current position to the point at lookahead distance
position_la_vector = np.array([lookahead_point[0] - self.position[0], lookahead_point[1] - self.position[1]])
yaw = self.position[2]
eta = np.arcsin(np.dot([-np.sin(yaw), np.cos(yaw)], position_la_vector)/np.linalg.norm(position_la_vector))
lat_acc = 2*target_speed**2 / lookahead_distance * np.sin(eta)
steering_angle = self.steer_lookup.lookup_steer_angle(lat_acc, target_speed)
ack_msg.drive.steering_angle = steering_angle
ack_msg.drive.speed = np.max(target_speed, 0) # no negative speed
Dynamic Bicycle Model
타이어의 종방향(x) 힘과 횡방향(y) 힘을 계산한다.
\[\begin{align*} F_{xp_f} &= C_{\tau_f}\tau_{x_f} \\ F_{yp_f} &= C_{\alpha_f} \left(\delta_f - \dfrac{v_y + I_f \psi}{v_x} \right) \\ F_{xp_r} &= C_{\tau_r} \tau_{x_r} \\ F_{yp_r} &= - C_{\alpha_r}\left( \dfrac{v_y - I_r \psi}{v_x} \right) \end{align*}\]다음과 같다.
\[F_{xf} = F_{xp_f} \\ F_{xr} = F_{xp_r} \\ F_{yf} = F_{yp_f} \\ F_{yr} = F_{yp_r} \\\]따라서 다음의 종방향 운동 방정식, 횡방향 운동 방정식, yaw 회전 운동 방정식에 대입하자.
\[\begin{align*} m(\dot{v}_x) - \dot{\psi}v_y &= F_{xf} + F_{xr} \\ m(\dot{v}_y) + \dot{\psi}v_x &= F_{yf} + F_{yr} \\ I_z \ddot{\psi} &= I_f F_{yf} - I_r F_{yr} \end{align*}\]