[Cart Pole] Motor Controller and State Observer
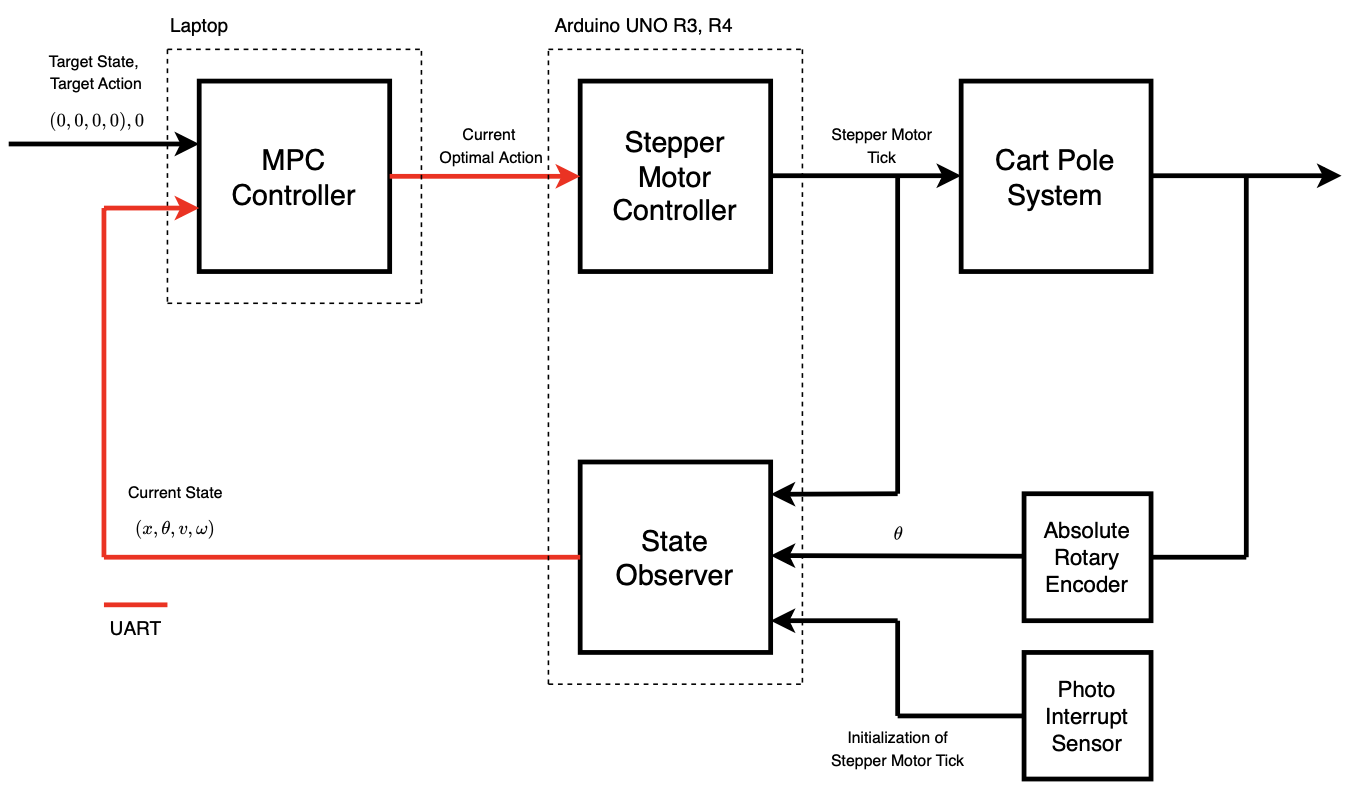
Stepper Motor Controller
모터 제어에 있어 기본 설정 값은 다음과 같다.
섬세한 제어를 하기 위해 12상 여자 방식을 사용하여 제어한다. 12상 여자 방식은 모터가 한 바퀴 회전하는 데 400 step이 필료하다. 또한 반지름이 0.01m인 timing pulley를 사용한다. 따라서 $400 \Delta x = 2 \pi (0.01m)$로부터 모터가 한 step 이동할 때 움직인 거리는 다음과 같다. 이때 step이라는 차원은 m와 같은 거리라는 것을 주의하자.
\[\Delta x = 0.000175m\]Arduino에서 64 분주의 타이머를 사용한다. Arduino UNO R3가 16M Hz의 clock spped를 제공하므로 64분주의 타이머를 사용할 때 1 clock period는
\[\Delta t = 1/(16M/64) = 4 us\]MPC는 50ms마다 최적의 현재 선가속도를 제시한다. 이에 맞게 stepper motor의 상을 잡아줘야 한다.
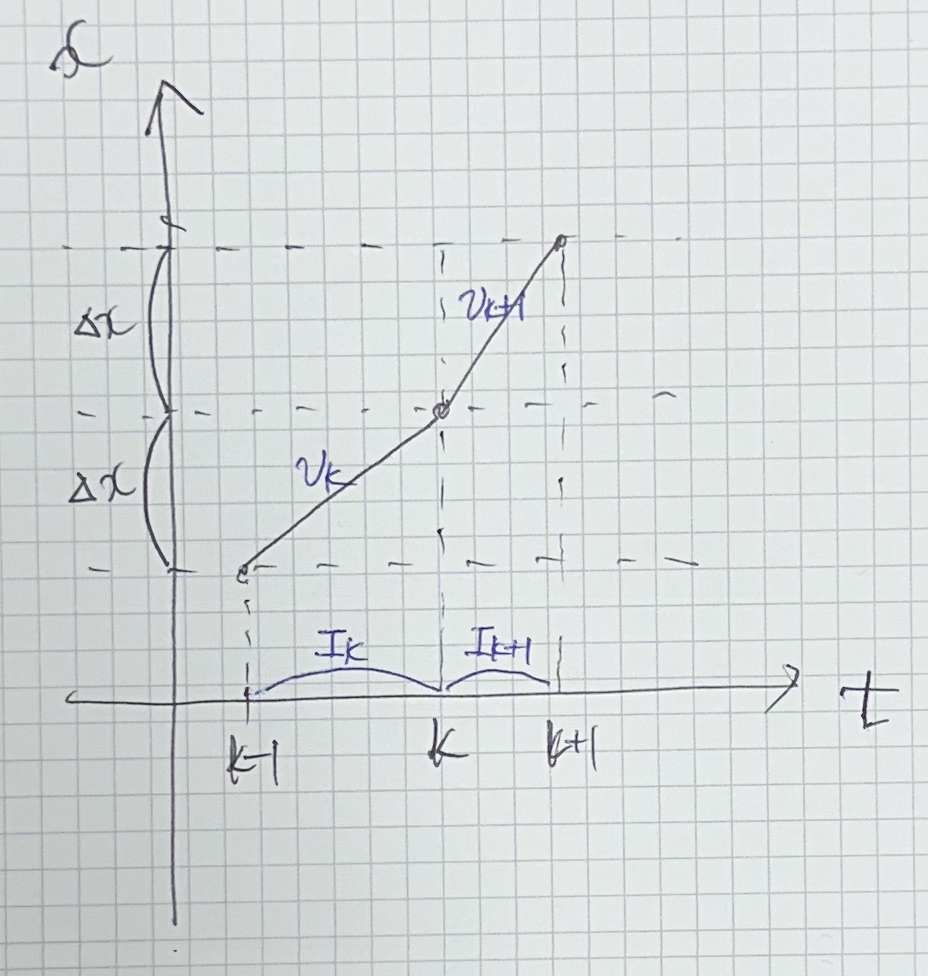
현재 시점은 k라 하고, 마지막으로 모터를 제어한 시점을 k-1, 다음으로 모터를 제어할 시점을 k+1이라고 하자. 그러면 k-1부터 k까지 이동한 거리와 k부터 k+1까지 이동한 거리는 $\Delta x = 0.000175 m$로 동일하다.
k-1부터 k까지 걸린 시간(s)을 $I_k$, k부터 k+1까지 걸린 시간(s)을 $I_{k+1}$이라고 하고, 각각의 시간에 대응하는 clock의 개수(count)를 $I_k’, I_{k+1}’$라고 하자. 또한 각각의 구간에서 속도(m/s)를 $v_k, v_{k+1}$라고 하자.
다음의 관계가 성립한다. 이때 $I_k$의 단위는 s이고, $I_k’$의 단위는 count이다.
\[\begin{align} I_k = 0.000004s \times I_k', \;\;\; I_{k+1} = 0.000004s \times I_{k+1}' \end{align}\]$v_k$와 $I_{k+1}$의 관계를 다음과 같이 구할 수 있다.
\[\begin{align} v_k = \dfrac{\Delta x}{I_k}, \;\;\; v_{k+1} = \dfrac{\Delta x}{I_{k+1}} \end{align}\]MPC controller로부터 현재 시점 $k$에서 최적의 가속도 $a_k$가 주어진다. 우리의 목표는 그 가속도에 해당하는 현재 시점 k부터 다음 시점 k+1 사이의 clock의 개수(count) $I_{k+1}’$를 구하는 것이다.
주어진 가속도$(m/s^2)$ $a_k$로부터 $v_{k+1}$를 다음과 같이 근사할 수 있다.
\[\begin{align} v_{k+1} = v_k + a_k I_k \end{align}\]식 (2)을 식 (3)에 대입하자.
\[\dfrac{\Delta x}{I_{k+1}} = \dfrac{\Delta x}{I_k} + a_k I_k\]$I_{k+1}$에 대해 정리하자.
\[\begin{align*} I_{k+1} &= \dfrac{\Delta x}{\dfrac{\Delta x}{I_k} + a_k I_k} \\ &= \dfrac{I_k}{1 + a_k I_k^2 / \Delta x} \\ \end{align*}\]이에 식 (1)을 대입하여 $I_{k+1}’$에 대해 정리하면 $I_{k+1}’$에 대한 update 식을 얻을 수 있다. 이때 모든 단위는 SI 단위로 통일한다.
\[\begin{align*} I_{k+1}' &= \dfrac{I_k'}{1 + a_k (4 \mu s \cdot I_k')^2 / \Delta x} \\ &= \dfrac{I_k'}{1 + a_k ((0.000004s) \cdot I_k')^2 / (0.000175 m)} \\ &= \dfrac{I_k'}{1 + (0.000004^2 / 0.000175)(a_k /(m/s^2)) I_k'^2} \\ &= \dfrac{I_k'}{1 + (9.142857e-8)(a_k /(m/s^2)) I_k'^2} \\ &= \dfrac{(10 937 500.171) I_k'}{(10 937 500.171) + (a_k /(m/s^2)) I_k'^2} \\ \end{align*}\]State Observer
\[\mathbb{x}(k) = \begin{bmatrix} x_1(k) \\ x_2(k) \\ x_3(k) \\ x_4(k) \\ \end{bmatrix} = \begin{bmatrix} x(k) \\ \theta(k) \\ v(k) \\ \omega(k) \\ \end{bmatrix}\]- $x$ : Position of Cart
- $\theta$ : Angle of Pole
- $v$ : Velocity of Cart
- $\omega$ : Angular Velocity of Pole
In order to apply the NMPC strategy, we must bave access to the state at time $k$.While the state of cart position $x(k)$ and pole angle $\theta (k)$ are measured directly by stepper motor and encoder sensor respectly, we need to estimate the cart velocity $v(k)$ and pole angular velocity $w(k)$. We simply approximate the time derivatie via a finite difference approximation.
\[\omega(k) = \dfrac{\theta (k) - \theta (k-1)}{T}\]