[Cart Pole] Nonlinear Model Predictive Control
Dynamics
Dynamic Equation
Assumption
- Cart와 rail 사이의 마찰력은 무시한다.
- 공지 저항은 무시한다.
- Cart와 pole은 모두 질량 분포가 일정하여 pole의 중력이 pole의 기하학적 중심에 작용한다고 가정한다.
Nomenclature
- $x$ : Distance of cart from initial position [$m$]
- $\theta$ : Tilt angle of rod [$rad$]
- $M$ : Mass of Cart [$kg$]
- $m$ : Mass of rod [$kg$]
- $I$ : Inertia of rod [kg $\cdot m^2$]
- $L$ : Length of rod [$m$]
- $F$ : Force applied at cart [$N$]
뉴턴 역학을 이용해서 inverted pendulum을 모델링할 수 있다.
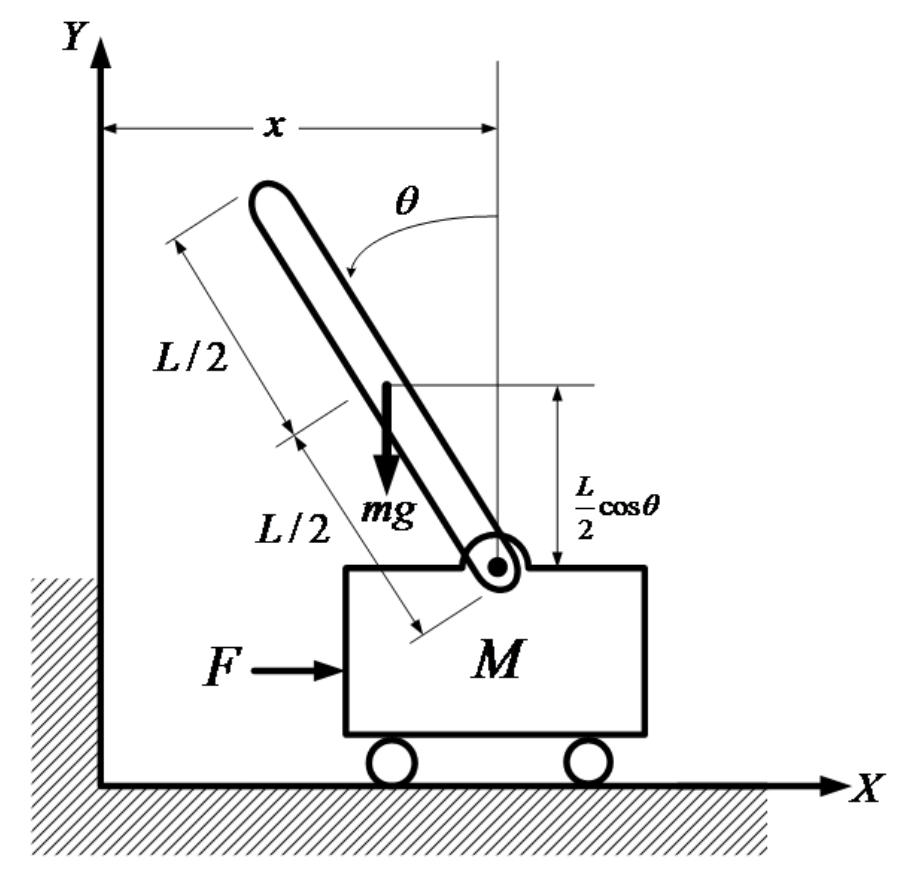
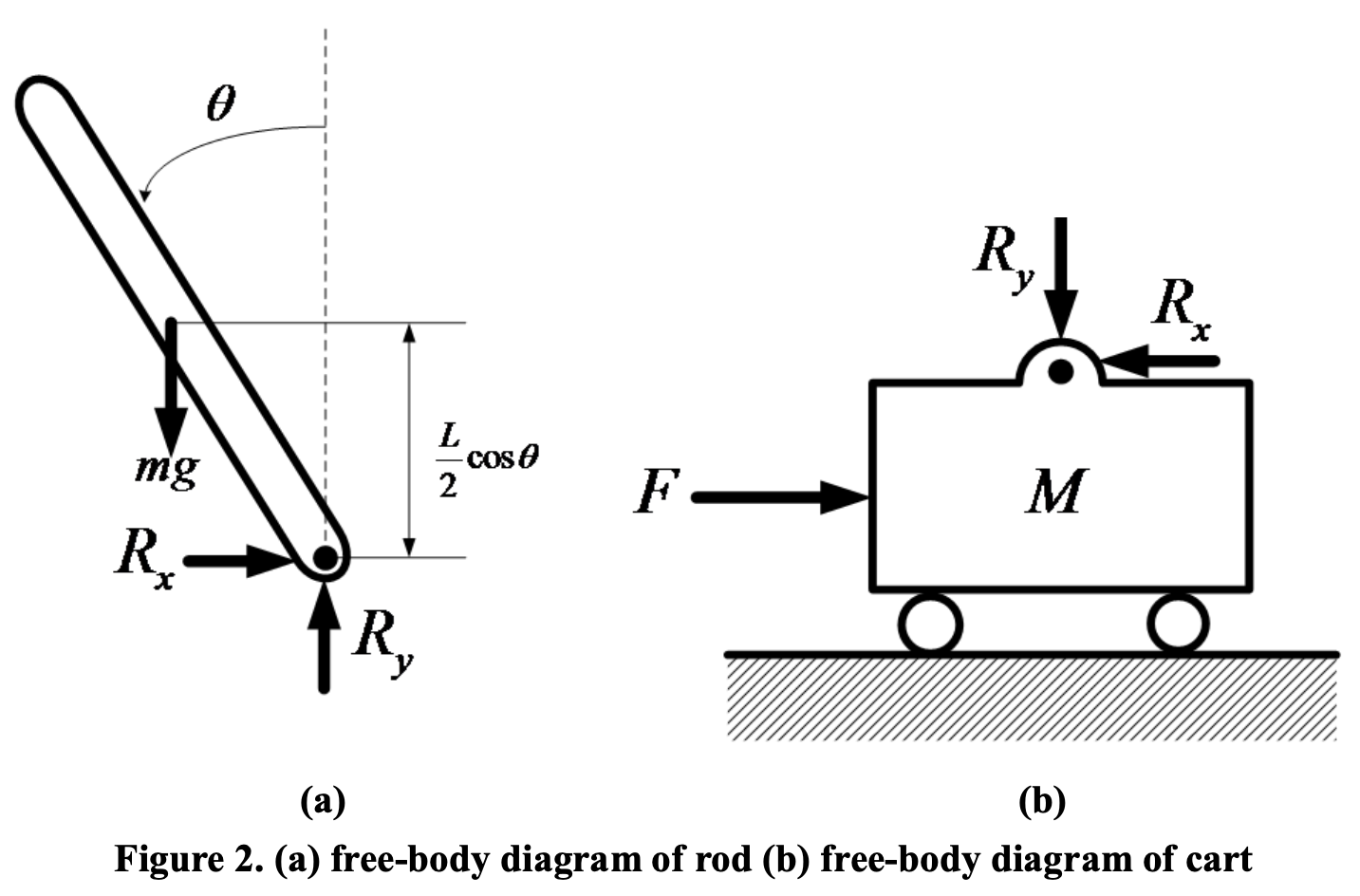
카트와 막대 간의 반력을 $R$라 정의하자.
Cart와 pole을 하나의 계로 잡고 뉴턴 운동 법칙을 적용하자.
$$
\begin{align}
& F = R_x = (M + m) a \\
\end{align}
$$
Pole 계에 대해 뉴턴 운동 법칙을 적용하자.
$$
\begin{align}
& \sum F'_x = R_x = m\ddot{x}_m \\
& \sum F'_y = R_y - mg = m \ddot{y_m} \\
\end{align}
$$
Cart 계에 대해 뉴턴 운동 법칙과 돌림힘 법칙을 적용하자.
$$
\begin{align}
& \sum F_x = F - R_x = M\ddot{x} \\
& R_x \dfrac{L}{2} \cos\theta + R_y \dfrac{L}{2}\sin\theta = I\ddot{\theta} \\
\end{align}
$$
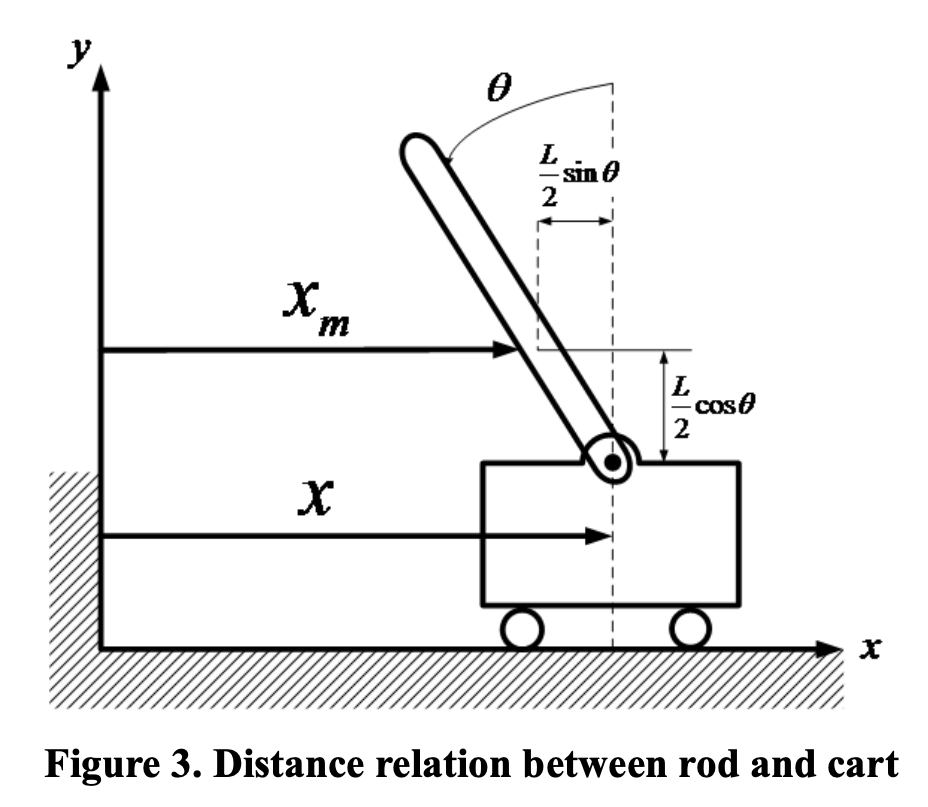
위 그림에서 $x$와 $x_m$ 간의 관계를 얻을 수 있다.
$$
\begin{align}
& x_m = x - \dfrac{L}{2} \sin\theta \\
& y_m = \dfrac{L}{2} \cos\theta \\
\end{align}
$$
6, 7번 식을 미분한다.
$$
\begin{align*}
& \dot{x}_m = \dot{x} - \dfrac{L}{2} \dot{\theta} \cos\theta \\
& \dot{y}_m = -\dfrac{L}{2} \dot{\theta} \sin\theta \\
& \ddot{x}_m = \ddot{x} + \dfrac{L}{2} \dot{\theta}^2 \sin\theta - \dfrac{L}{2} \ddot{\theta} \cos\theta \\
& \ddot{y}_m = -\dfrac{L}{2} \dot{\theta}^2 \cos\theta - \dfrac{L}{2} \ddot{\theta} \sin\theta
\end{align*}
$$
이를 2, 3번 식에 대입한다.
$$
\begin{align*}
R_x
&= m \left[ \ddot{x} + \dfrac{L}{2} \dot{\theta}^2 \sin\theta - \dfrac{L}{2} \ddot{\theta} \cos\theta \right] \\
&= m \ddot{x} + m \dfrac{L}{2} \dot{\theta}^2 \sin\theta - m \dfrac{L}{2} \ddot{\theta} \cos\theta \\
R_y
&= mg + m \left[ -\dfrac{L}{2} \dot{\theta}^2 \cos\theta - \dfrac{L}{2} \ddot{\theta} \sin\theta \right] \\
&= mg - m \dfrac{L}{2} \dot{\theta}^2 \cos\theta - m \dfrac{L}{2} \ddot{\theta} \sin\theta
\end{align*}
$$
이를 4, 5번 식에 대입한다.
$$
\begin{align*}
& F = (M + m) \ddot{x} + m \dfrac{L}{2} (\dot{\theta}^2 \sin\theta - \ddot{\theta} \cos\theta) \\
& I \ddot{\theta} = mg\dfrac{L}{2} \sin\theta + m \dfrac{L}{2} \ddot{x} \cos\theta - m \left( \dfrac{L}{2} \right)^2 \ddot{\theta} \\
\end{align*}
$$
연립 방정식을 풀자.
$$
\begin{align*}
\ddot{\theta}
&= \dfrac{1}{(M+m) \left( I + m (L/2)^2 \right) - m^2 (L/2)^2 \cos^2\theta} \left[ -m^2 \left(\dfrac{L}{2}\right)^2 \dot{\theta}^2 \sin\theta \cos\theta + (M + m) mg \dfrac{L}{2} \sin\theta + m \dfrac{L}{2} \cos\theta F \right] \\
\ddot{x}
&= \dfrac{1}{(M+m) \left( I + m (L/2)^2 \right) - m^2 (L/2)^2 \cos^2\theta} \left[ m^2 \left(\dfrac{L}{2}\right)^2 g \sin\theta \cos\theta - m \left(I + m \left(\dfrac{L}{2}\right)^2 \right) \dfrac{L}{2} \dot{\theta}^2 \sin\theta + \left(I + m \left(\dfrac{L}{2}\right)^2 \right) F \right] \\
\end{align*}
$$
정리하면 다음 식을 얻는다.
$$
\begin{align*}
\ddot{\theta}
&= \dfrac{-m \dfrac{L}{2} \dot{\theta}^2 \sin\theta \cos\theta + \left[ M + m \right] g \sin\theta + F\cos\theta}{\dfrac{2}{mL} \left[ M + m \right] I + \dfrac{L}{2} \left[ M + m \sin^2\theta \right]} \\
\ddot{x}
&= \dfrac{mg\sin\theta \cos\theta - \left[ \dfrac{2}{L}I + m \dfrac{L}{2} \right]\dot{\theta}^2 \sin\theta + \left[ \dfrac{4}{mL^2} I + 1\right] F}{\dfrac{4}{mL^2}\left[ M + m \right] I + \left[ M + m \sin^2\theta \right]}
\end{align*}
$$
Continuous State Space Model
상태 변수와 입력을 다음과 같이 정의한다.
$$
\mathbb{x}(t) =
\begin{bmatrix}
x(t) \\
v(t) \\
\theta(t) \\
w(t) \\
\end{bmatrix} =
\begin{bmatrix}
x(t) \\
\dot{x}(t) \\
\theta(t) \\
\dot{\theta}(t) \\
\end{bmatrix} =
\begin{bmatrix}
x_1(t) \\
x_2(t) \\
x_3(t) \\
x_4(t) \\
\end{bmatrix}
, \;\;\;
u(t) = F(t)
$$
그러면 정리한 식을 $\dot{x} = f(x, u)$ 꼴의 비선형 상태 공간 모델로 나타낼 수 있다.
$$
\begin{align*}
\dot{x_1} &= x_2 \\
\dot{x_2} &= \dfrac{mg\sin x_3 \cos x_3 - \left[ \dfrac{2}{L}I + m \dfrac{L}{2} \right] x_4^2 \sin x_3 + \left[ \dfrac{4}{mL^2} I + 1\right] u}{\dfrac{4}{mL^2} \left[ M + m \right] I + \left[ M + m \sin^2x_3 \right]} \\
\dot{x_3} &= x_4 \\
\dot{x_4} &= \dfrac{-m \dfrac{L}{2} x_4^2 \sin x_3 \cos x_3 + \left[ M + m \right] g \sin x_3 + u \cos x_3}{\dfrac{2}{mL} \left[ M + m \right] I + \dfrac{L}{2} \left[ M + m \sin^2 x_3 \right]} \\
\end{align*}
$$
이를 $\dot{x} = f(x) + g(x) u$ 꼴로 나타내자.
$$
\begin{bmatrix}
\dot{x_1} \\
\dot{x_2} \\
\dot{x_3} \\
\dot{x_4} \\
\end{bmatrix}
=
\begin{bmatrix}
x_2 \\
\dfrac{mg\sin x_3 \cos x_3 - \left[ \dfrac{2}{L}I + m \dfrac{L}{2} \right] x_4^2 \sin x_3}{\dfrac{4}{mL^2} \left[M + m \right] I + \left[ M + m \sin^2x_3 \right]} \\
x_4 \\
\dfrac{-m \dfrac{L}{2} x_4^2 \sin x_3 \cos x_3 + \left[ M + m \right] g \sin x_3}{\dfrac{2}{mL} \left[ M + m \right] I + \dfrac{L}{2} \left[ M + m \sin^2 x_3 \right]} \\
\end{bmatrix}
+
\begin{bmatrix}
0 \\
\dfrac{\dfrac{4}{mL^2} I + 1}{\dfrac{4}{mL^2} \left[M + m \right] I + \left[ M + m \sin^2x_3 \right]} \\
0 \\
\dfrac{\cos x_3}{\dfrac{2}{mL} \left[ M + m \right] I + \dfrac{L}{2} \left[ M + m \sin^2 x_3 \right]} \\
\end{bmatrix}
u
$$
Discrete State Space Model
The above model describes the dynamic behavior in continuous-time. However, the required format for the NMPC controller is a discrete-time model.
To achieve the requiredment, we sample the continuous-time system using Euler’s method: this is done at a much faster rate than the control interval to provide better accuracy.
Forward Euler Method를 이용하면 다음과 같이 미분 방정식을 차분 방정식으로 바꿀 수 있다.
샘플링 주기를 $T$라 하자.
$$
\dot{x} = f(x, u), \;\;\; x_{k+1} = x_k + T \cdot f(x_k, u_k) \\
$$
$$
\begin{bmatrix}
x_1^{k+1} \\
x_2^{k+1} \\
x_3^{k+1} \\
x_4^{k+1} \\
\end{bmatrix}
=
\begin{bmatrix}
x_1^{k} \\
x_2^{k} \\
x_3^{k} \\
x_4^{k} \\
\end{bmatrix}
+
T
\begin{bmatrix}
x_2^k \\
\dfrac{mg\sin x_3^k \cos x_3^k - \left[ \dfrac{2}{L}I + m \dfrac{L}{2} \right] {x_4^k}^2 \sin x_3^k}{\dfrac{4}{mL^2} \left[M + m\right] I + \left[ M + m \sin^2x_3^k \right]} \\
x_4^k \\
\dfrac{-m \dfrac{L}{2} {x_4^k}^2 \sin x_3^k \cos x_3^k + \left[M + m \right]g \sin x_3^k}{\dfrac{2}{mL} \left[M + m \right] I + \dfrac{L}{2} \left[ M + m \sin^2 x_3^k \right]} \\
\end{bmatrix}
+
T
\begin{bmatrix}
0 \\
\dfrac{\dfrac{4}{mL^2} I + 1}{\dfrac{4}{mL^2} \left[M + m \right] I + \left[ M + m \sin^2x_3^k \right]} \\
0 \\
\dfrac{\cos x_3^k}{\dfrac{2}{mL} \left[M + m \right] I + \dfrac{L}{2} \left[ M + m \sin^2 x_3^k \right]} \\
\end{bmatrix}
u
$$
Optimisation
Dynamic Model
Dynamic model does not capture the whole situation physically.
Dynamic Model은 다음과 같이 단순화되었다.
- cart와 rail 사이의 마찰력은 무시한다.
- 공지 저항은 무시한다.
- cart와 막대는 모두 질량 분포가 일정하여 막의 중력이 막대의 기하적 중심에 작용한다고 가정한다.
- Inertia of pole이 cart와 pole의 질량과 pole의 길이에 비해 충분히 작으므로 pole의 enertia는 무시한다. ($I = 0$)
- mass of cart ($M$) : 0.123kg (122.61g)
- length of cart : 0.045 m (4.5cm)
- mass of pole ($m$) : 0.089kg (88.68g)
- length of pole ($L$) : 0.4m (40cm)
- inertia of pole ($I$) : 0.004746 kg m^2
- length of rail : 0.72 m (72cm)
- maximum magnitude of force (N) : 1.2 N
$$
\begin{bmatrix}
\dot{x_1} \\
\dot{x_2} \\
\dot{x_3} \\
\dot{x_4} \\
\end{bmatrix}
=
\begin{bmatrix}
x_2 \\
\dfrac{mg\sin x_3 \cos x_3 - m \dfrac{L}{2} x_4^2 \sin x_3}{M + m \sin^2x_3} \\
x_4 \\
\dfrac{-m \dfrac{L}{2} x_4^2 \sin x_3 \cos x_3 + \left[ M + m \right] g \sin x_3}{\dfrac{L}{2} \left[ M + m \sin^2 x_3 \right]} \\
\end{bmatrix}
+
\begin{bmatrix}
0 \\
\dfrac{1}{M + m \sin^2x_3} \\
0 \\
\dfrac{\cos x_3}{\dfrac{L}{2} \left[ M + m \sin^2 x_3 \right]} \\
\end{bmatrix}
u
$$
Cost Function
\[\underset{u}{\mathrm{minimize}} \;\;\; \sum^{N-1}_{i=0} \left[ \mathbb{x}^T(k + i) Q \mathbb{x}(k + i) + u^T(k + i) R u(k + i) \right]\]We would like the state $x(k)$ to be at the origin, which corresponds to the cart position at the centre of the beam, the cart not moving, the pendulum angle of 0 radian (upright), and the pendulum not rotating.
Futhormore, we would like to be economical with control action and thus penalise input movements. This objective can be described in terms of the cost function via the choice.
\[Q = \begin{bmatrix} q_1 & 0 & 0 & 0 \\ 0 & q_2 & 0 & 0 \\ 0 & 0 & q_3 & 0 \\ 0 & 0 & 0 & q_4 \\ \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 10 & 0 & 0 \\ 0 & 0 & 10^{-4} & 0 \\ 0 & 0 & 0 & 10^{-4} \\ \end{bmatrix}, \;\;\; R = r = 0.1\]- Since it is important the the pendulum angle is zero, $q_2$ receives a high value.
- It is less important that the cart position is zero, so $q_1$ has the next highest value.
- Cart velocity and pendulum angular velocity are not so important, so $q_3, q_4$ receive a low value.
Constraints
Importantly, there are physical limits on the control input and the cart position, which correspond to constraints on the supply current to the motor and the length of the beam respectively.
\[\underline{u} \leq u(k) \leq \overline{u} \\ \begin{bmatrix} -0.36 \\ -\infty \\ -\infty \\ -\infty \\ \end{bmatrix} \leq \mathbb{x}(k) \leq \begin{bmatrix} 0.36 \\ +\infty \\ +\infty \\ +\infty \\ \end{bmatrix}\]Optimisation Problem
상위 제어기는 매 step마다 다음의 최적화 문제를 푼다.
- Current step : k = 0
- Control Sampling Period : T = 50ms (20Hz)
- Horizon : N = 10
$$
\begin{bmatrix}
x_1(k+1) \\
x_2(k+1) \\
x_3(k+1) \\
x_4(k+1) \\
\end{bmatrix}
=
\begin{bmatrix}
x_1(k) \\
x_2(k) \\
x_3(k) \\
x_4(k) \\
\end{bmatrix}
+
T
\begin{bmatrix}
x_2(k) \\
\dfrac{mg\sin x_3(k) \cos x_3(k) - m \dfrac{L}{2} {x_4(k)}^2 \sin x_3(k)}{M + m \sin^2x_3(k)} \\
x_4(k) \\
\dfrac{-m \dfrac{L}{2} {x_4(k)}^2 \sin x_3(k) \cos x_3(k) + \left[M + m \right]g \sin x_3(k)}{\dfrac{L}{2} \left[ M + m \sin^2 x_3(k) \right]} \\
\end{bmatrix}
+
T
\begin{bmatrix}
0 \\
\dfrac{1}{M + m \sin^2x_3(k)} \\
0 \\
\dfrac{\cos x_3^k}{\dfrac{L}{2} \left[ M + m \sin^2 x_3(k) \right]} \\
\end{bmatrix}
u
$$